分类问题和回归问题的区分：

看y值：

分类问题：目标值是离散性的，比如男女大小

回归问题：目标值是连续的，在一定区间内任意取值，比如房价

KNN算法：

基本思想：

根据距离函数计算待分类样本 X 和每个训练样本的距离作为相似度，选择与待分类样本距离最小的K个样本未为“最邻近”，以K个最邻近中大多数所属的类别作为X的类别。（少数服从多数 / 权重投票法）

优缺点：

优点：

• 无需估计参数、无需训练
• 对噪声数据不敏感
• 适合对稀有事件进行分类

缺点：

• 时间复杂度为O(m*n)，m属性个数，n样本数

决策树

基本思想：

通过特征选择准则（如信息增益、信息增益比、Gini指数等）递归划分数据，分裂节点优先选择“区分度“最高的属性。自上而下内部节点属性比较，叶节点得出结论。

通过决策树算法计算属性权重：

• 基于分裂次数 / 深度：次数越多说明属性越重要，分裂深度越小权重越高
• 基于特征选择准则值：选择信息增益或者GIni指数下降值作为权重1，值越大表示属性越重要。
• 集成方法扩展：通过随机森林（多个决策树集成）对属性重要性进行统计，比如平均每个树中属性的分裂贡献。

这种属性权重计算方法优势：

• 可解释性强
• 与分类任务高度贴合
• 对非线性友好：决策树能捕捉属性与类别间非线性、高阶交互关系
• 易于实现：主流机器学习库如 scikit-learn 内置了决策树/随机森林的特征重要性计算接口，如 fearture_importance，可以直接调用。

决策树三种算法：

• ID3 通过 信息增益 进行划分，ID3在特征取值比较多时可能过拟合泛化性减弱
• C4.5 通过 信息增益比 进行划分，弥补 ID3 的缺陷
• CART 通过 Gini指数 进行划分，

贝叶斯分类算法

基本思想：

已知类条件概率密度参数表达式和先验概率，利用贝叶斯公示转换成后验概率，根据后验概率大小进行决策分类。

朴素贝叶斯方法通过假设所有的属性都是独立的，避免计算属性上的联合概率。 问题转化为如何计算p(X|Ci)

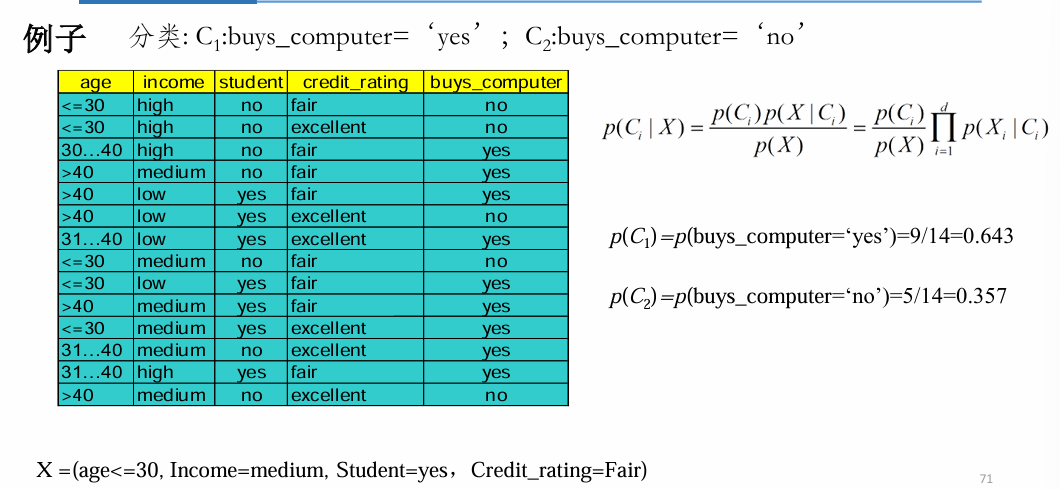
优缺点：

优点：

• 分类概率稳定
• 对小规模的数据表现良好
• 对缺失数据不敏感，算法简单

缺点：

• 模型假设属性之间相互独立，在属性个数比较多或者属性相关性比较大的时候分类效果不好，在属性相关性较小时朴素贝叶斯性能最为良好。

随机森林

高级分类算法，集成多个学习器（决策树），个体学习器间不存在强依赖关系，随机森林在bagging基础上做了修改。

• 从样本集中用Bootstrap采样选出 n个样本；
• 从所有属性中随机选择k个属性， 选择最佳分割属性作为节点建立 CART决策树；
• 重复以上两步m次，即建立了m 棵CART决策树；
• 这m个CART形成随机森林，通 过投票表决结果，决定数据属于 哪一类。

具有需要调整的参数少，不容易 过度拟合，分类速度快，能高效 处理大样本数据等特点；

随机森林（RF）通过同时改变 样本和特征子集来获得不同的弱 分类器。

支持向量机 SVM

是一种有监督的学习方法，SVM的雏形是感知机模型。

• 模型定义：

• 损失函数：